La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
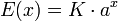
siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
| Gráfica de Funciones exponenciales | |
| Definición | 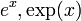 |
|---|---|
| Tipo | Función real |
| Dominio |  |
| Codominio | 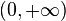 |
| Imagen | 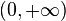 |
| Propiedades | Biyectiva Convexa Estrictamente creciente Trascendente |
No hay comentarios:
Publicar un comentario